[ベスト] y(4x y)dx-2(x^2-y)dy=0 667205-Y(4x+y)dx-2(x^2-y)dy=0

Simple and best practice solution for (Xy^2x)dx(yx^2y)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkAnswer to (e^x y)dx (2 x ye^3)dy = 0, y(0) = 1 (4y 2x 5)dx (6y 4x 1) dy = 0, y(1) = 2 (3y^2 x^2/y^5)dy/dx x · Not exact If it is exact then (2y 1/ x cos 3x ) dy (y/x^2 4x^3 3y sin 3x) dx = 0 Which can be thought of as df(x,y) = C = f_y \ dy f_x \ dx = 0 If so, the mixed partials should be equal f_(yx) = 1/x^2 color(red)() 3 sin 3x f_(xy) = 1/x^2 color(red)() 3 sin 3x So this is not exact

Solve The Differential Equation X Y 2 X Dx Y X 2 Y

Y(4x+y)dx-2(x^2-y)dy=0

Y(4x+y)dx-2(x^2-y)dy=0-D/dx x^2 y^4, d/dy x^2 y^4 Extended Keyboard;The equation is M(x,y)dx N(x,y)dy =0 with M = 4xy y^2 , M_y = 4x 2y N = 2y 2x^2 , N_x = 4x # M_y The equation is not exact , but (N_x M_y)/M = 2/y , depends only on y The integrating factor is 1/y^2 and leads to the equation P(x,y

How To Solve The Differential Equation 2y 3xy 2 Dx X 2x 2y Dy 0 Quora

Simple and best practice solution for y(4xy)dx2(x^2y)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it · Homework Statement Solve 6x^2*y^2*dx4x^3*y*dy=0 Homework Equations This is an exact equation The Attempt at a Solution Here's my work 6x^2*y^2*dx=4x^3*y*dy 1/x dx=2/3*1/y*dy ln abs(x)C=2/3*ln abs(y) 1/y^(2/3)=Cx y^(2/3)=1/(Cx) xy^(2/3)=1/C C=1/(xy^(2/3)) But the answer in the book$M~dx N~dy = 0$ $y(4x y)~dx 2(x^2 y)~dy = 0$ $M = y(4x y) = 4xy y^2$ $N = 2(x^2 y) = 2x^2 2y$ $\dfrac{\partial M}{\partial y} = 4x 2y$

Click here👆to get an answer to your question ️ Solve x^2y dx (x^3 y^3) dy = 0Solve ( dy(x))/( dx) (x x^2 y(x)^2) x y(x)^2 y(x) = 0 Let y(x) = sqrt(v(x))/x, which gives ( dy(x))/( dx) = sqrt(v(x))/x^2 (( dv(x))/( dx))/(2 x sqrt(v(xSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

This is a first order differential equation in differential form The method of exact equations starts by writing the ODE in this form math2xydx (y^2 x^2)dy = 0/math is the same as the ODE math\frac{dy}{dx} = \frac{2xy}{(y^2 x^2)}/Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition73 Solve x 4 x 2 y 4 2y 4 = 0 In this type of equations, having more than one variable (unknown), you have to specify for which variable you want the equation solved We shall not handle this type of equations at this time

Math 432 Hw 2 5 Solutions Pdf Free Download

The Solution Of Y 2x 2y E X Dx E X Y 3 Dy 0 If Y 0 1 Is Sarthaks Econnect Largest Online Education Community

Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more · first you need to seperate the individual variables Y dy = 4x dx then you integrate both sides 1/2*y^2 = 2*x^2 C given y(2) = 2 you can solver for CFind the general solution of y^2dx (x^2 – xy y^2) dy = 0 asked Sep 21, in Differential Equations by Chandan01 ( 512k points) differential equations

Solve The Differential Equations 2x Y 1 Dx 4x 2y 1 Dy 0 Sarthaks Econnect Largest Online Education Community

Questions On Exact And Non Exact Equations Zill 8 Edition 05 Subtraction Elementary Mathematics

 · I dy/dx I 3x^2 y = Ix^2 recall that according to the product rule d/dx( Iy) = I dy/dx y dI/dx, this implies that in the above equation we can rewrite I dy/dx = d/dx(Iy) y dI/dx, which gives d/dx(Iy) y dI/dx I 3x^2 y = Ix^2, consolidate the second and third terms on the left hand sideSimple and best practice solution for (4xxy^2)dx(yx^2y)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itI'm at the beggining of a differential equations course, and I'm stuck solving this equation $$(x^2y^2)dx2xy\ dy=0$$ I'm asked to solve it using 2 different methods I proved I can find integrating factors of type $\mu_1(x)$ and $\mu_2(y/x)$If I'm not wrong, these two integrating factors are $$\mu_1(x)=x^{2} \ \ , \ \ \mu_2(y/x)=\left(1\frac{y^2}{x^2}\right)^{2}$$ Then, I've used $\mu

Solved 1 Solve The Bvp 6xy 4 Dx 3x 2y Dy 0 Y 2 4 Chegg Com

How To Solve 3x Xy 2 Dx X 3 2y Dy 0 Quora

 · Ex 96, 11 For each of the differential equation find the general solution 𝑦 𝑑𝑥 𝑥− 𝑦﷮2﷯﷯𝑑𝑦=0 Step 1 Put in form 𝑑𝑦﷮𝑑𝑥﷯ Py = Q or 𝑑𝑥﷮𝑑𝑦﷯ P1 x = Q1, y dx (x − y2) dy = 0 y dx = − (x − y2)dy 𝑑𝑦﷮𝑑𝑥﷯ = −𝑦﷮𝑥− 𝑦﷮2﷯﷯ This is not of the form 𝑑𝑦﷮𝑑𝑥﷯ Py = Q ∴ we find(4x – 3y)dx (2y – 3x)dy = 0 4xdx 2ydy – 3(xdy ydx) = 0 4xdx 2ydy – 3d(xy) = 0 Integrating, we get 2x 2 y 2 – 3xy = c which is the required solution ofSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

3 8 Implicit Differentiation Calculus Volume 1

How To Do Implicit Differentiation 7 Steps With Pictures

To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `(3x yy^2)dx(x^2x y)dy=0`Simple and best practice solution for y(xy2)dxx(yx4)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

Solving Separable Differential Equations Calculus Socratic

2x 5y 3 Dx 2x 4y 6 Dy Mathematics Stack Exchange

 · y = 2x^2c/x^2 > 2(y4x^2)dxxdy = 0 Which we can rearrange as follows dy/dx = (2 (y4x^2))/x " " = 8x(2y)/x dy/dx (2y)/x = 8x A We can use an integrating factor when we have a First Order Linear nonhomogeneous Ordinary Differential Equation of the form;Click here👆to get an answer to your question ️ Solve (x^2 y^2) dx 3xy dy = 0$(x^2y^2)dx−2xydy=0$ $\frac{dy}{dx}=\frac{x^2y^2}{2xy} $(i) This is a homogeneous differential equation because it has homogeneous functions of same degree 2 homogeneous functions are $(x^2y^2)$ and $2xy$, both functions have degree 2 Solution of differential equation Equation (i) can be written as,

Doc Differential Equations Tt Arafat Rahman Academia Edu

Solve The Following Homogenous Differential Equation X2y 2xy2 Dx X3 3x2y Dy 0 Brainly In

2 (2xy)dx(x6y)dy=0 Ej 24 Ecuaciones exactas Alexander Estrada Solución de problemas del libro "Ecuaciones diferenciales con problemas con valores enCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historySolve y(4xy)dx 2(x^2y)dy = 0 by finding the integrating factor and test for exactness Expert Answer Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculator

Solved Evaluate The Following Differential Equations Variable Separable Homogeneous Equation X 2 Y 4x 2 7xy 2y 2 2 Exact Equation Cos X Si Course Hero

Solution Of X 2 4xy 2y 2 Dx Y 2 4xy 2x 2 Dy 0 Is

08 · μ(y) = e^∫(2/y dy) μ(y) = y^2 Multiplying by μ(y) (y^22xy)dx (x^2) dy = 0 (12x/y)dx ( x^2/y^2)dy = 0 Confirm that the equation is now exact, and you're on your way Both partials = 2x/y^2 finding the solution So we now have an exact equation (12x/y)dx ( x^2/y^2)dy = 0 Again giving these things some names M(x,y) = 12xSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreDy/dx P(x)y=Q(x) Then the integrating factor is given by;

How To Solve The Differential Equation 2y 3xy 2 Dx X 2x 2y Dy 0 Quora

3 8 Implicit Differentiation Calculus Volume 1

Find dy/dx y^2(y^24)=x^2(x^25) Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate using the Product Rule which states that is where and By the Sum Rule, the derivative of with respect to isI = e^(int P(x) dx) \ \ = exp(int \ 2/x \ dx) \ \ =Find the particular solution of the differential equation (1 y^2)(1 log x) dx 2xy dy = 0 given that y = 0 when x = 1 asked Mar 17 in Differential Equations by Takshii (

Differential Equatio Long Answer Questions 7 M R Solye 2x Y 3 Dx

Solve The Following Differential Equations A Xdy Y Dx I X Dx Y Dy 2

 · "The solution is" \qquad \quad \ ln 4 y^2 4 x y 4 x^2 \ = \ 2 sqrt{ 3 } arctan( { x 2 y }/ { \sqrt{ 3 } x } ) C # "We are asked to solve the differentialSimple and best practice solution for 2y(x^2yx)dx(x^22y)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkShow that the differential equation $(12x^2y^24xy^3)dx(22x^3y4x^2y^2)dy=0$ is not exact, but admits integrating factor $\mu=\mu(xy)$ Find $\mu$ and solve the equation With the method

Engineering Mathematics Notes

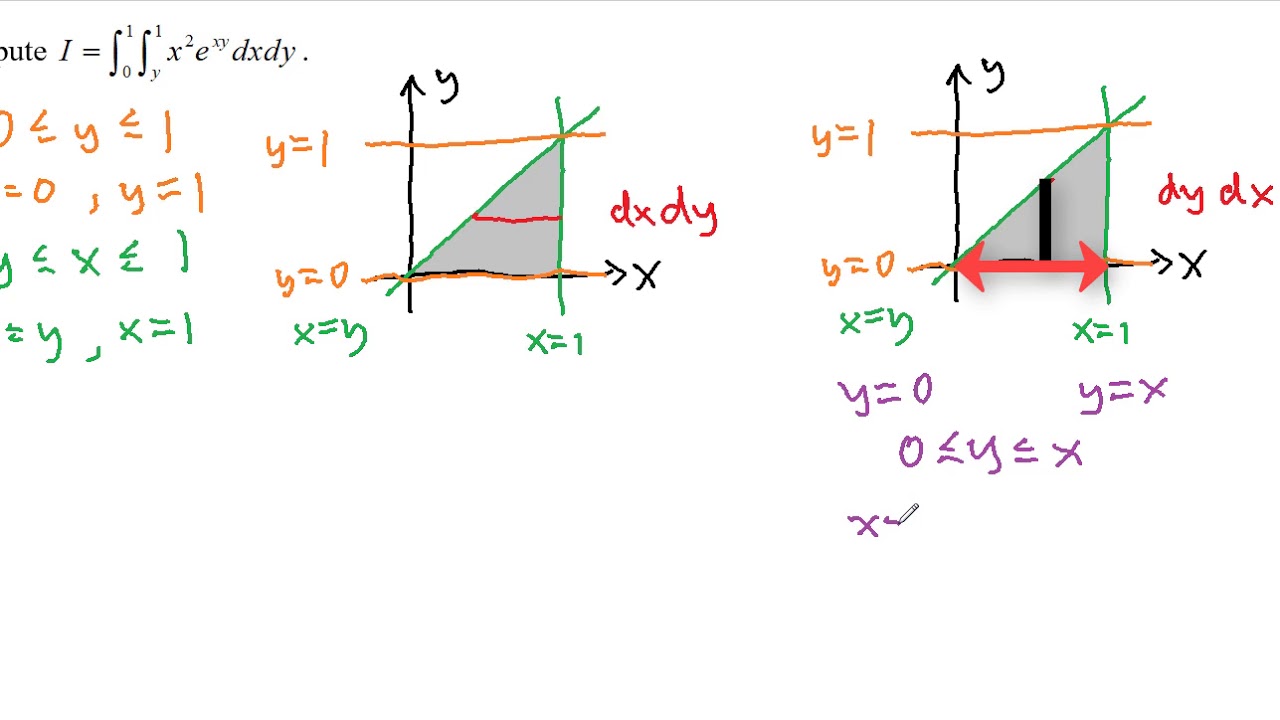
Double Integrals Volume And Average Value

Suppose a dependent variable y represents a function f of an independent variable x, that is, = () Then the derivative of the function f, in Leibniz's notation for differentiation, can be written as (())The Leibniz expression, also, at times, written dy/dx, is one of several notations used for derivatives and derived functionsA common alternative is Lagrange's notationMath(2x y) dx (4x y 6) dy = 0/math Find substitutions mathu, t/math to remove the math(6)/math mathy = u a, x = t b/math math\frac{duEquations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations (2x^2y)dx(x^2yx)dy=0 so that you understand better

How To Solve 1 4xy 2 Dy Dx Y 3 Quora

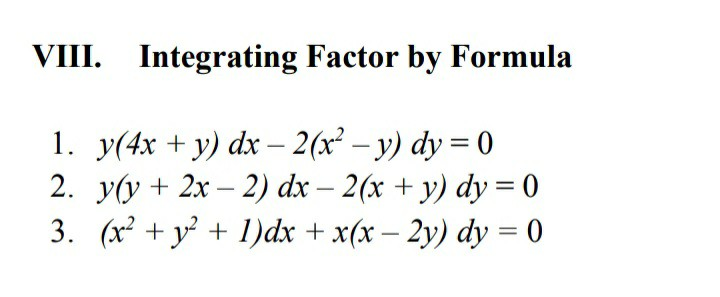
Solved Viii Integrating Factor By Formula 1 Y 4x Y D Chegg Com

The equation can be written as M(x,y)dx N(x,y)dy =0 with M = 6yx^2 4x , N = 2x^3 6y , M_y = N_x = 6x^2 The equation is exact ie is the total differential dF(x,y)=0 solved by F_x = M = 6yx^2 4x F_y = N = 2x^3 6y Integrating the first

Solved Y 4x Y Dx 2 X 2 Y Dy 0 Solve This Give Me Explanation And Clear Writings Course Hero

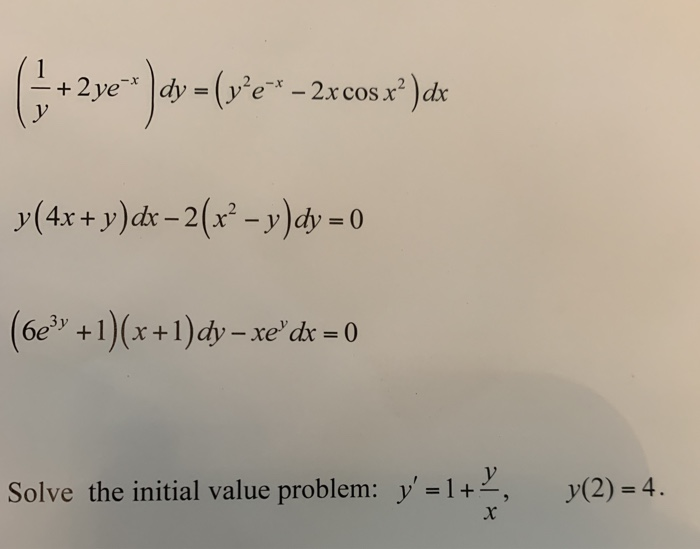
Solved 2ye Dy V E 2x Cos Xº Dx Y 4x Y Dx Chegg Com

For Solving Dy Dx 4x Y 1 Suitable Substitution Is Youtube

If X2 Y2 2 Xy Find Dy Dx Mention Each And Every Step Mathematics Topperlearning Com Gwvwfskk

2x 3y X 2y See How To Solve It At Qanda

Let Y 4x 2 Find The Differential Dy When X 5 And Dx 0 4

Answered Use The Mixed Partials Check To See Bartleby

How To Solve Dy Dx 4x Y 7 2x Y 1 Quora

X 2 4xy 2y 2 Dx Y 2 4xy 2x 2 Dy 0 Brainly In

Exact Non Differential Equation

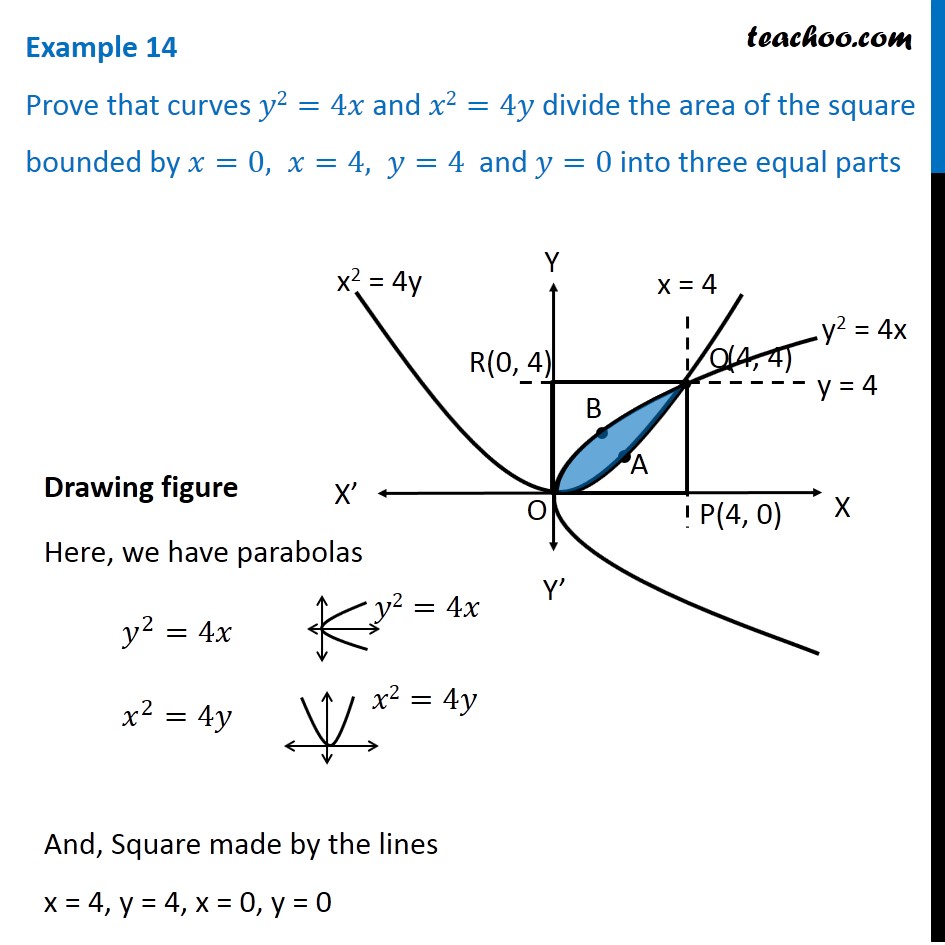
Example 14 Prove That Y2 4x X2 4y Divide Area Of Square

Lesson 6 Exact Equations Determine Whether Or Not Each Of

Solve The Differential Equation X Y 2 X Dx Y X 2 Y

Solved In Problems 31 Through 42 Verify That The Given D Chegg Com

3y 2 X b Dx 2y Y 2 3 b Dy 0 Admits An Integrating Factor Which Is A Function Of X Y 2 Mathematics Stack Exchange

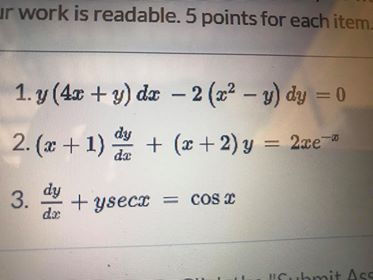
Solved Ur Work Is Readable 5 Points For Each Item 1 Y Chegg Com

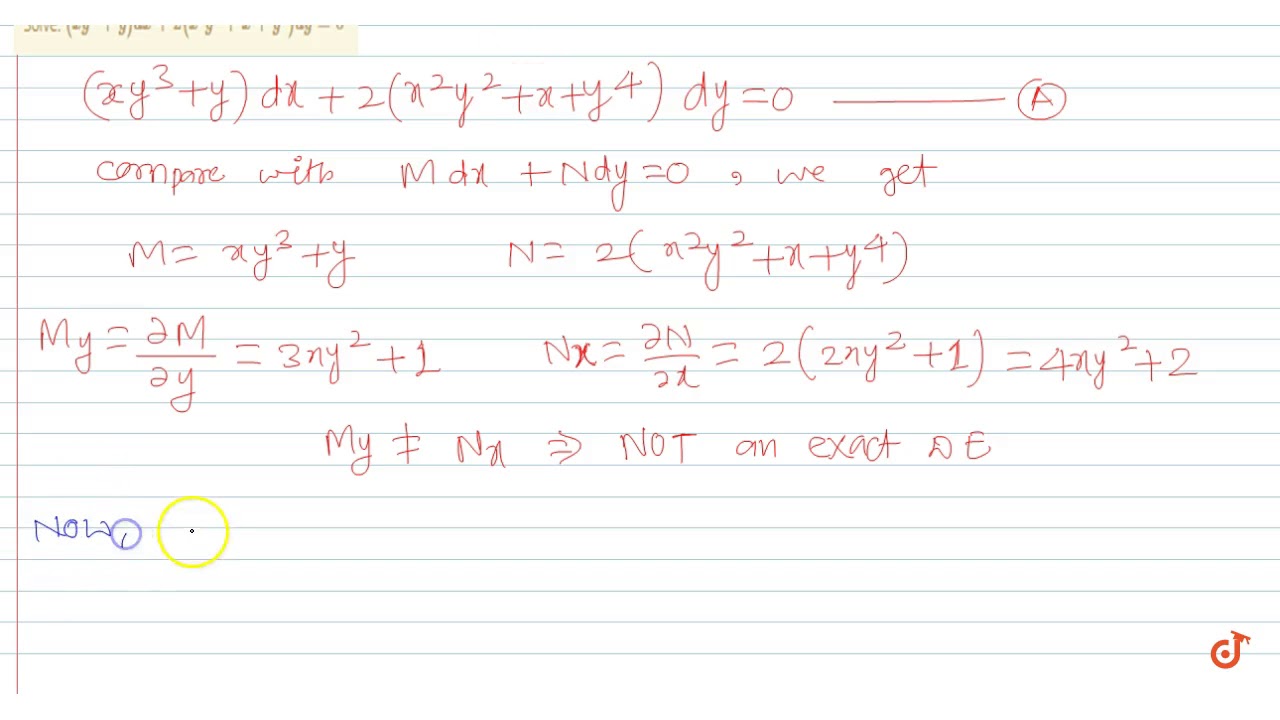
Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube

Solved Obtain The Particular Solution Satisfying The Init Chegg Com

Math 432 Hw 2 5 Solutions Frostburg

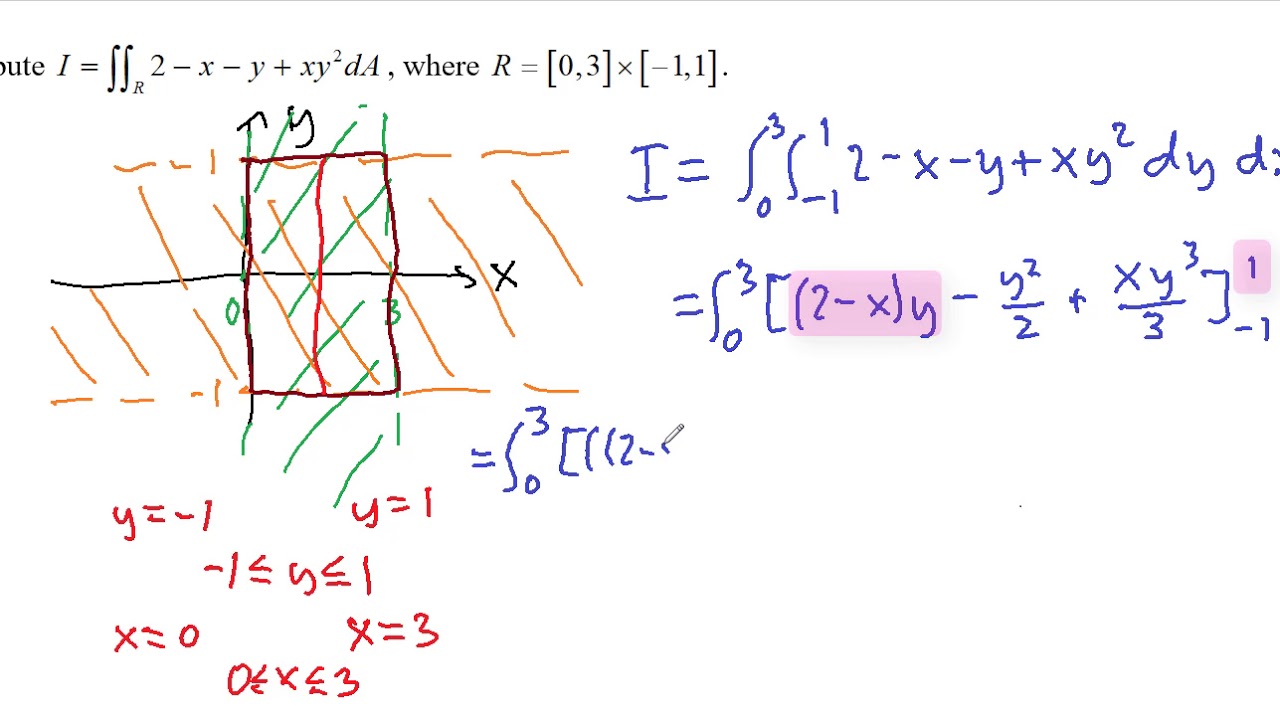
Double Integrals Volume And Average Value

Differential Equations Shepley L Ross

Solucionarioecuacionesdiferencialesdenniszill7aedicion P

Math 432 Hw 2 4 Solutions Frostburg

4 Solve The Exact Differential Equation 1 2xy Dx 4y3 X2 Dy 0 4 Solve The Exact Differential Equation Homeworklib

How To Solve Exact Differential Equations In Matlab Stack Overflow

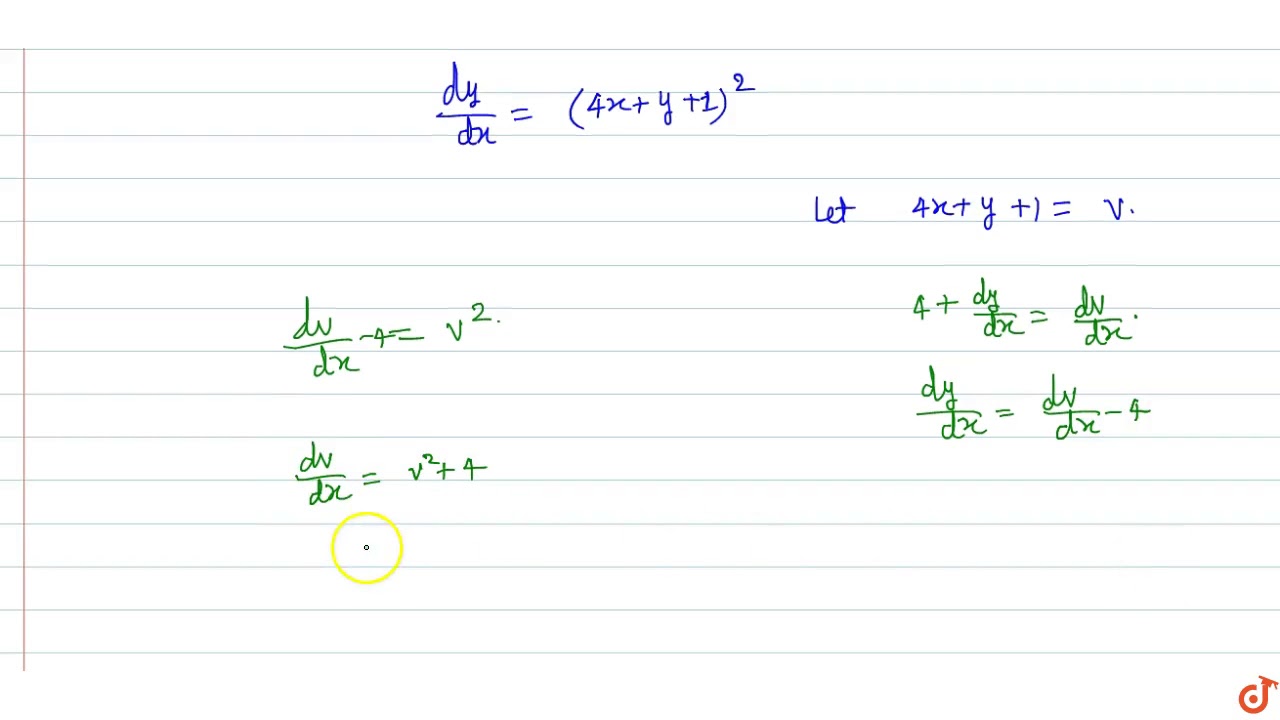
Dy Dx 4x Y 1 2 Youtube

Bt Ptvp Xuan Sv Moi

Ch 2 6 Exact Equations Integrating Factors Consider A First Order Ode Of The Form M X Y N X Y Y 0 Suppose There Is A

Mth 311 Lecture 3 Ch2 Intro To Diff Eq S Continued Oneclass

Help With Differential Equations Having Problems With The 2nd Problem 3rd 6th 7th And The Rest I Don 39 T Understand How To Work The 2nd 3rd 6th And The Rest Of The Questions

Engineering Mathematics Notes

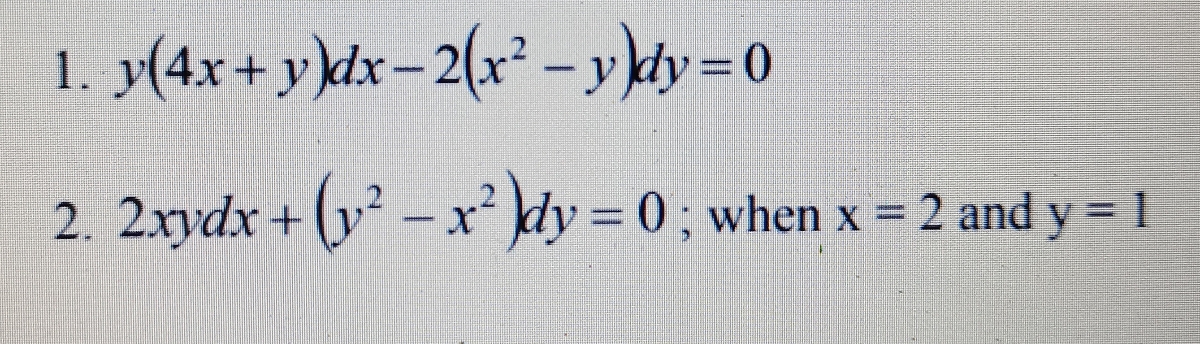
Answered 1 Y 4x Y Dx 2 X Y Kdy 0 2 Bartleby

Solve This Plzzz 18 Find The Equations Of The Normal To The Curve Y 4x3 The Line 19 Maths Integrals Meritnation Com

Solve 3xy 2ay 2 Dx X 2 2axy Dy 0 Mathematics Stack Exchange

The Integrating Factor Of Y4 2y Dx Xy3 2y4 4 Aspirebuzz

Tutorial 4 Question For Solution By Substitutions Studocu

Answered 2 Prove The Following 1 F X Y Is Bartleby

Worked Example Identifying Separable Equations Video Khan Academy

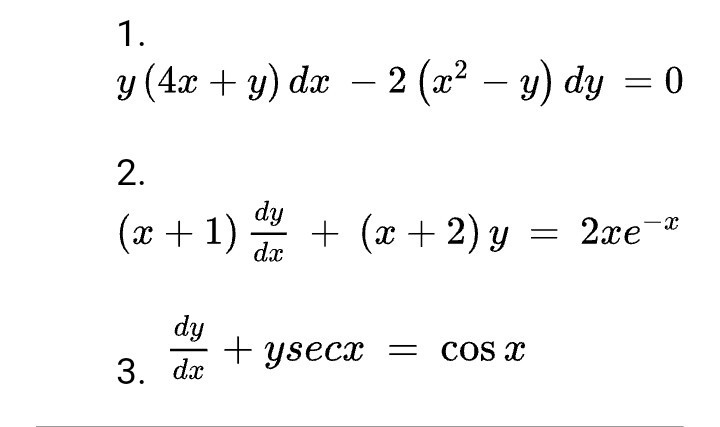
Solved 1 Y 4x Y Dx 2 X2 Y Dy 0 2 X 1 X Chegg Com

Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation

Solutions To Homework 2 Introduction To Differential Equations

How To Solve The Differential Equation 2x Y Dx 4x Y 6 Dy 0 Quora

Mth 311 Lecture 3 Ch2 Intro To Diff Eq S Continued Oneclass

4xy 3y 2 X Dx X X 2y Dy Brainly In

Example 21 Find General Solution Ydx X 2y2 Dy 0

Pdf 2 6 Exact Differential Equations And Integrating Factors Mirna Mansour Academia Edu

Verifying Solutions To Differential Equations Video Khan Academy

Math 432 Hw 2 5 Solutions

Solve The Differential Equation Dy Dx Square 4x Y 1 Youtube

Differential Equations Solved Examples 17

Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube Dubai Khalifa

Engineering Mathematics Notes

3 X2 4xy 2y2 Dx Y2 4xy 2x2 D See How To Solve It At Qanda

Incoming Term: y(4x+y)dx-2(x^2-y)dy=0,